算数能力理論モデル
(Campbell,J.I.D.,Epp,L.J: Architectures for Arithmetic. Pp347-360,In;Campbell(ed):Handbook of Mathematical
Cognition,2005 Psychology Pressより)
認知的アーキテクチャーとはなにか?
特定のドメインの認知的アーキテクチャーを特異化するため処理段階、又はモジュールを規定する。
例えば、3+4=?を一連の処理段階に分解する。
1) 刺激を適切な内的コードに変換する
2) 答えの想起又は計算
3) 答えの産出
この分解がコード-化の認知的サブシステムを構成するアーキテクチャーを意味する。
最も基本的な問題は、段階が独立しており、足し算的であるのか、あるいは総合的で相互作用的であるのかどうか、という点である。
もし、2つ段階が足し算的ならばこれはそれぞれの段階がその操作を独立して遂行することを意味する。
相互的又は足し算的符号化−想起メカニズムの問題は重要−決定的である。それは、数処理の認知的及び神経心理学的研究の双方の方法、理論的方向に影響する。
3つのアプローチ
算数の符号化及び計算の段階は厳密に足し算的段階と言うよりは相互作用的である。
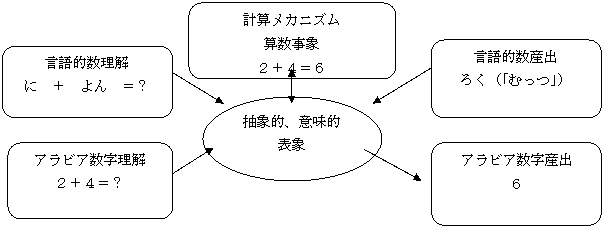
抽象的コードモデルAbstract Code Model
McClosky,1992
Mcclosky & Macaruso,1994
Sokol, Mcclosky, Cohen, & Aliminosa, 1991
3つの認知的タイプ
理解
計算
回答産出システム
このモデルの中心はこれらのサブシステムがひとつの抽象的、意味的量コードの共有を通じて交流する、と主張することである。
プロセスの独立性
図20.1 Mcclosky(1992)の抽象的コードモデル
 |
トリプルコードモデルTriple code Model
Dehaene 1992,
Dehaene & Cohen 1895
この理論は、数処理が行われる3つのコードがあると仮定する。
・an Analogue magunitude represdentation
・a Visual-Arabic number Form
・an Auditory-Verbal Code System
抽象的コードモデルとは対照的に、3つのコードは抽象的な、a modal codeとは交渉することなしに相互に、直接に活性化すると仮定することである。
しかし、抽象的コードモデルと同様に、各要素は異なる数処理課題に寄与すると仮定する。
Analogue-magnitude codeは概数の計算と推測数の大きさの比較を支援し、おそらくsubitizing(一目で認知すること)で役割を演じる。
Digital inputとout put及びmulti-digit operationはアラビア数形式(Arabic form)によって媒介される。
聴覚−言語コードは書字及び口頭入力と出力を媒介し、簡単は足し算とかけ算の事象に表象の基礎を提供する。
抽象的コードモデルが言語に依存しない処理を仮定しているのに対してトリプルコードモデルは数事象の記憶に、言語に基づく表象を仮定する。
中枢的抽象的コードが仮定しないにもかかわらず、DehaeneとCohenのトリオプルコードモデルは相互的ではなく、足し算的符号化/想起処理を指示する。
トリプルコードモデルではいったん入力が適切なコードに変換されると処理は入力の形に関係なく、同じ様式で生じる。
通称的コードモデルと同様、トリプルコードモデルの符号化と計算処理ははっきりと足し算的である。
トリプルコードモデル
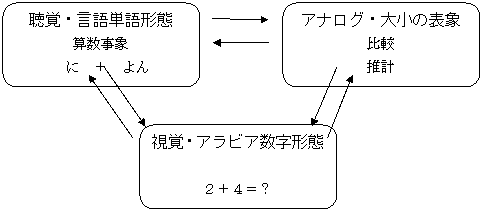
図20.2 Dehaene & Cohen’s(1995) triple code model
符号化−複合仮説
Encoding-Complex Hypothesis
Cambell and Clark, 1988,1992
Cambell, 1992,1994
Clark & Cambell,1991
Cambell とClarkは数処理の基礎的減少はそうした単純な足し算的アーキテクチャーでは表現されないことを指摘した。
“符号化コンプレックス”の観点は競合的数反応と操作間の相互干渉の解決が有能な数認知にとって、土台である、とする実験結果によって示唆された。
数はいろいろの数機能と密接に連携している。(たとえば、数の読み、または転移符号化(トランスコーディング−注:他のモジュール符号への変換)、数比較、推量、算数事象)
結論的に言えば、数は自助的に与えられた課題の文脈で重要な情報が重要でない豊富な連携のネットワークを活性化する情報を含んでいる。
成功するパフォーマンスは、この重要でない情報からの干渉の克服を必要とする。
たとえば、有能な大人が足し算、かけ算を早く、という指示の元で行うとき、彼らが行うエラーは干渉の過剰、(plethora of influency)を明らかにする。
エラーは通常、関連する操作力、関連する操作(3*6=21)、又は関連する操作(3*6=9)、にける実際的隣接を含む。
エラーはしばしば問題の演算(the problem operands)(eg. 2+9=9)のひとつによる、又は先行する思考で想起された回答による侵襲(intrusion)を頻繁に含む。
さらにエラーはそうした要因が特別の思考への作用と結びつく時生じやすい。
エラーを増大させる要因は正答への時間を増大させる。それは干渉の解決が重い要因であることを示す。
さらに、これらの要因の影響は表面tきフォーマット(アラビア文字vs数単語)によって大きく変化する。
Encoding-complexの観点ではこれらの現象の重要性はそれらが潜在的に数処理に寄与するモジュールシステムがしばしば足し算的にではなく、相互作用的に交流していることを示していることである。
トリプルコードモデルにおけるようにencode-complex的観点は数処理がひとつ又は複数の表象コードにおける情報の課題特異的な活性化を含んでいると見る。
しかし、encode-complex的観点は加えて表象システム間の交流がしばしば厳格に足し算的プロセスであるよりは相互作用的プロセスを含むことを想定する。
相互作用プロセスは課題特異的な実践の産物である。それは干渉への抵抗を最適化するため、システム内およびシステム間の興奮抑制の結合を創造する。
そうした統合的な符号化−想起手続きの発達が有能な数処理を獲得する基礎的メカニズムである。
したがって、有能な処理の概念はencode-complex仮説の核心である。