目次
□現象的特徴
□算数障害の歴史
□数処理のモジュール性
□多要素的な数処理の特性
□コード変換、単一コード変換ルートモデル、複数コード変換ルートモデル
□算数障害の理論モデル
□
算数・計算困難(算数・計算障害)の現象的特徴
算数障害は必ずしも算数(数学)が出来ないことではありません。高等数学が良くできる人(数学専攻の大学院生など)に算数障害があることがあるといわれています。難しい数式は解けるのに、簡単な数の操作ができない(自分の電話番号が覚えられれないなど)ことが起きたりするのです。
算数・計算障害の困難さは、反復訓練によって回復するような算数・計算のスキル困難にあるわけではありません。
多くの基礎的な認知機能でつまずいている場合があります。
1,算数、数学用語の問題。
学校算数には子どもが日常あまり使わないことばが1年生のはじめからいっぱい出てきます。 算数では算数独特の言葉が多く使われます。
たす、ひく、よりおおい、より少ない、〜こずつ、円、半径、辺、直線、割る、かける、分数、分母、分子などなど。
2,方向性
数字は、普通左から右に読みます。計算は、右(一の位)から左に進みます。10のくらいの1は10を表します。11は、10と1で、「じゅういち」と読みますが、101ではありません。
3,順序
2567と2657は違います。短期記憶の弱い子どもは、順序を理解することがにがてでよく混乱します。
4,「花子さんは太郎さんよりアメを3つ多くもっています。」といわれても、多いのはどちらかわかりません。
×−5=3という計算は、左から計算することはわかりますが、左から考えること は出来ません。計算方法の問題ではなく、方向性の問題です。
3nは、×がないのに、なぜかけ算なのか、丁寧な視覚的な説明が必要です。
5,計算の仕方はわかっていても、早くするようにいわれると混乱してしまいます。
6,独特のストラテジーを発見し、身につけていることがあります。
”答えは「=」の前の数字より、ひとつ少ない”(6−3=2)という方略をもっている子がいます。この方略を何にでもあてはめます。9−3=6という答えを自分で出した後、「ほんとは”2”なのに(3よりひとつ少ないのは2)へんだ」)
T.Rマイルズらは、算数障害は言語関連障害であると言っています。読み書き障害のメカニズムと同じ混乱が生じていると考えています。数、計算という抽象的なものを具体的なもの、視覚的に把握できるものに置き換えて提示すると、直観的に理解できるようになることがあります。
ページTOPに戻る
算数障害の歴史
獲得性計算障害の詳細で体系的な最初のケースの記述はHenschen(1919)による。彼は、その際、”Akalkulie”という用語を選択した。Henschenは、”Akalkulie”は様々な形態で現れるとした。
Henschen以前にも、神経心理学分野での計算障害の報告はあったが、たいていは他の障害に随伴して生じると考えられていた。Lewandowsky/Stadelmann(1908)は、脳障害の結果としての計算障害をはじめて記述した。Hecaenと共同研究者は多くの論文で、Akalukulieを三つのサブタイプに分類した。
(a)読み又は書き障害の結果としてのAkalkulie
(b)筆算の差異の空間障害としての結果としてのAkalkulie
(c)算数操作の実行の歳に現れる障害であるいわゆるAnarithmetie(失計算)
(Hecaene/Ang4lerques1961;Luria,1973)
Gerstmann(1927,1940)ははじめてGyrus
anguria近辺の領域の障害後に計算障害を示した患者を報告した。計算障害は、手指失認、失行症、左右障害と結びついていた。こうした計算障害は、他の障害(空間障害など)に付随して二次的に生じるものである、と言う見解がある。(Krapf,1937,Singer/Low,1933).Krapfはこうした計算障害を「構成的失計算」(knstruktive
Akaluklie)と名付けた。
ゲルストマン症候群が常に四つの症状を併せ持つかどうかについても疑問とする見解もあるようである。
参考文献
Landerl/Kaufmann:Dyskalkulie,
Reinhardt, 2008
乖離と二重乖離Dssoziation und
doppelte Dissoziation
機能Aが正常であり、機能Bが障害があるとき、乖離という。
二重乖離はある人が、機能Aが正常で機能Bが障害があり、他の人が逆に機能Bが正常であり、機能Aに障害があることをいう。二重乖離は認知心理学において、認知システムのモジュール構造の証明とされる。すなわち、機能Aと機能Bはそれぞれ独立していると考えられる。二重乖離の概念についてはカミロフ・スミスなどが発達的視点から、モジュール性そのものが先験的なものではなく、発達的に形成されるものであることを批判的に論じている。
計算障害における乖離現象
1,計算能力と一般知能の乖離
2,計算能力と言語能力の乖離
3,数的記憶と非数的記憶の乖離
4,数理解と数算出の乖離、又はアラビア数字と数単語の読みの乖離
5,様々な数操作の間の乖離
6,数的事象の知識と手続き的知識の乖離
多要素的な数処理の特性
数処理の中心的要素
算数は、多要素的な思考プロセスである。
つまり、数の取り扱いにあたって関与する。
認知神経心理学は、思考プロセスと認知能力を詳細に、システマティックに研究する。
4+2という計算でも、大人と子どもでは異なる思考回路とをとる。子どもは、多くの段階をへて、苦労しながら解決(答えは6)に至る。
大人は、計算プロセスを通らないで、自然に答えを出す。つまり、当たり前に、考えずに答えを出すのである。
従ってまず、数、及び計算システムの構造を明らかにする必要がある。いわば、子どもは多くの要素を含む数的思考プロセスをどのように一つ一つ身につけ、問題解決のひとつに操作にまとめ上げる能力を身につけていくのだろうか?
数システムの特殊性
①言語的数システムと書字的数システムの基本的違い
/ご/と<5>と<・・・・・>
②位
21と12と233の<2>の数的意味は、全てことなる。数字の順序の位置から理解する。
<2>は2であり、20であり、200である。
左から読むが、右からの順序である。
位取りシステムは、いかなる情報処理によって可能となるか?
③アラビア数システムの統語的性格
29と92のちがい
足し算的かかけ算的な統語構造
405は400+5か、100×4か
通常、構成規則としてはかけ算規則が足し算規則よりも早く習得される。
④コード変換(トランスコーディング)
数の読みと書きの間の変換
言語的数システムと視覚的数システムの間に変換
ニジュウゴ → 25、は言語的から視覚的への変換
25を読む(25→ニジュウゴ)は、視覚的から言語的への変換
コード変換の際の典型的なエラーは、統語的構造か、レキシカル要素に対応する。
統語的構造のエラー:405→4005と書く
レキシカル要素のエラー:405を407と書く。
(Deloche/Seron,1982a,b)
獲得性計算障害では、レキシカル要素のエラーは、読みあるいは言語障害と結びついているとき現れる。
408を48と書く場合
Grana et.al,2003
0の統語が生じる。40の倍常に生じる、しかし、40236ではエラーが起きない。
Granaらは、レキシカル要素0は統語的0よりも易しい、と解釈した。レキシカル要素0は10進法の意味的大きさと直接結びついているが、統語的0は無関係である。
⑤意味的と非意味的単一ルートモデルと多元的ルートモデル
コード変換、単一コード変換ルートモデル、複数コード変換ルートモデル
今日の論争的なテーマのひとつ
コード変換
ある数様式から他の数様式へのコード変換は常に、対応する数がその他得央する大きさで捉えられることを必要とするのかどうか、と言う問いが議論されている。
ここでは、意味的コード変換が、すなわち、数の意味への対応によるコード変換が問題となっている。
原理的に、数形態は意味的である、すなわち、意味理解無しには翻訳された数は得られない、と考えられる。通常の成人ではいかなる数形態であろうと、数意味は自動的に活性化される。
McCloskeyらのモデル(1985)は、あらゆるコード変換のプロセスが抽象的な内的(意味的な)表象を通じて進行する、と定式化した。
いわゆる、単一ルートモデル、である。
これに対して、いわゆるコード変換の複数ルートモデルは、意味的処理経路とともに非意味的処理経路を定立した。
(Cipolotto 1995,
Cipolotti/Butterworth 1995, Cohen et al 1994, Dehaene/Cohen1995)
意味的ルートと非意味的ルートの乖離を示すケースの報告
Cipolotti 1995のSF
数単語の形式(すなわち、正字法ルート)では、多位数の数を読めたが、アラビア数字形式では読めなかった。
これに対して、Cipolottiのたのケースは、言語的及び書字的出力を要求する課題で困難を示した。かれは、筆算では一位数と多位数を、暗算では二位数の正しく配置することができた。
両方のケースが、意味理解では一部無傷であることをしめした。すなわち、コード変換は数理解とは独立して傷害されるのである。
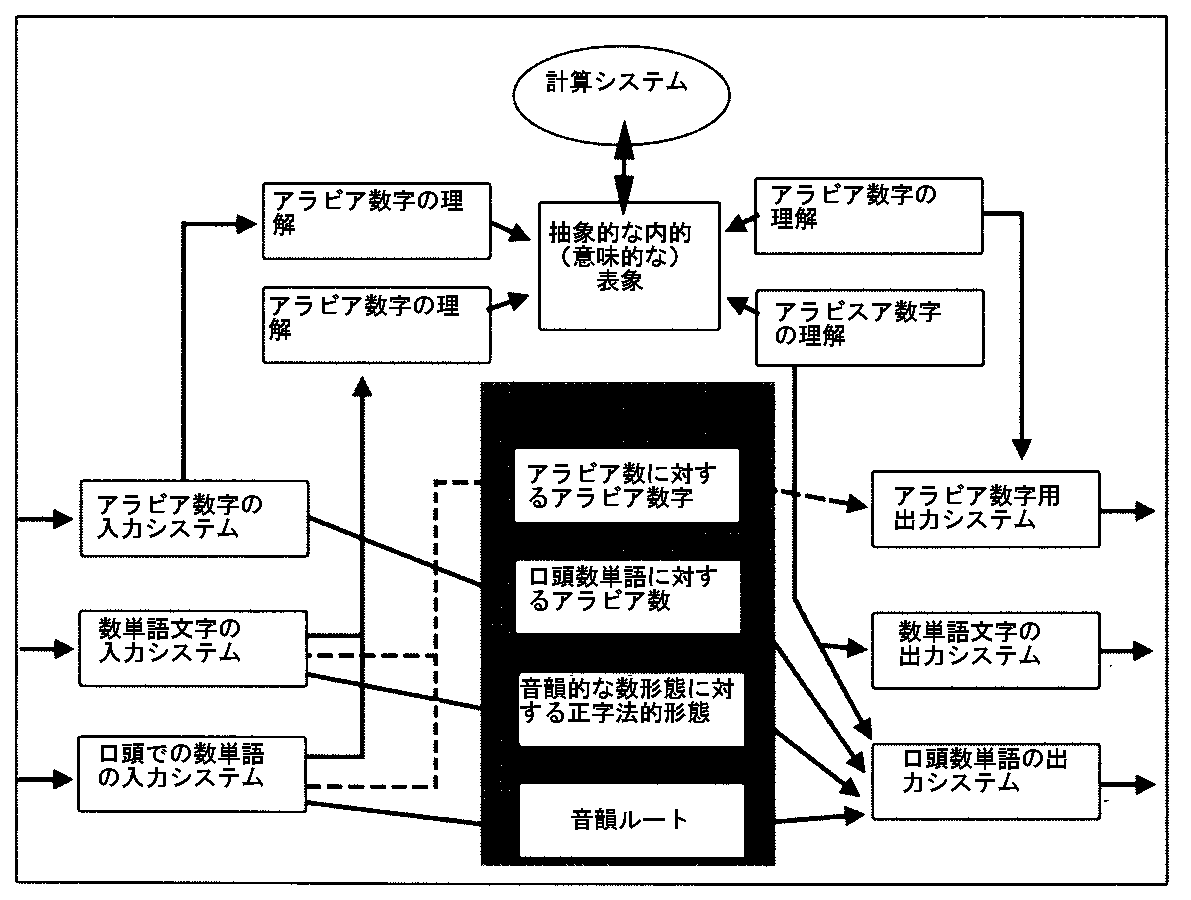
こうしたケース研究に基づいて、ButterworthとCipolottiは図のような複数コード変換モデルを開発した。
意味的コード変換に付随して生じる四つの区別可能な非意味的コード変換ルート。
・アラビア数字の読み書きを可能にする意味的コード変換ルート。
・数単語の復唱と読みを可能とする非意味的コード変換ルート。これらはかなり高い蓋然性で数だけでなく、一般的言語処理メカニズムに帰することができる。
| ButterworthとCipolottiの「複数コード変換モデル」 1995 | ||
 |
||
コード変換の複数ルートモデルは、二つの点で、McCloskeyモデル(1985,1992)と異なっている。
a)数単語の復唱も書取も、抽象的意味表象への関与を必要としない。
b)アラビア数字の読みにたいしても、書きにたいしても、意味的ルートのほかに直接的な非意味的コード変換ルートが存在する。